The first story regards George Bernard Dantzig, famous for the simplex algorithm and also one of the founders of linear programming. Here are Dantzig's own words:
During my first year at Berkeley I arrived late one day to one of Neyman's classes. On the blackboard were two problems which I assumed had been assigned for homework. I copied them down. A few days later I apologized to Neyman for taking so long to do the homework - the problems seemed to be a little harder to do than usual. I asked him if he still wanted the work. He told me to throw it on his desk. I did so reluctantly because his desk was covered with such a heap of papers that I feared my homework would be lost there forever.
About six weeks later, one Sunday morning about eight o'clock, Anne and I were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: "I've just written an introduction to one of your papers. Read it so I can send it out right away for publication." For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard which I had solved thinking they were homework were in fact two famous unsolved problems in statistics. That was the first inkling I had that there was anything special about them.
To be honest I don't really know which theorems are the ones mentioned in this story, but I found a paper of that time (1940) that should be the one mentioned in the story:
- G. B. Dantzig 1940. On the non-existence of tests of "Student's" hypothesis having power functions independent of σ, Annals of Mathematical Statistics, Volume 11, number 2, pp186-192
The second story regards a very nice theorem in differential geometry that I know well: the Fary-Milnor Theorem. The legend says that John Milnor (a classmate of the famous John Nash), was sleeping in class while the proffesor explained three unsolved problems in knot theory and when he woke up he copied from the blackboard the three problems (which he assumed were assigned as homework). A week later he turned in solutions for every problem!!! Among these problems was the Fary-Milnor theorem. This gives me an opportunity to discuss this nice theorem.
The curvature K (which should be the greek letter kappa) is a function with real values over some set C (which denotes a parametrization by arc length). This theorem says that if we calculate the total curvature (by doing the integration in the trajectory) then:
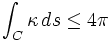if the parametrized curve C don't have any knots, this means that C can be deformed in to a circumference without been teared. Of course if C has knots then
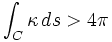Actually the total curvature is always bigger or equal than 2*pi and only equals 2*pi if C represents a circumference, just as we should expect. The formal statement of this result is the Fary-Milnor theorem.John Milnor would later receive the Fields Medal for his proof that a 7-dimensional sphere can have several differential structures (28 to be exact), this result opened the field of differential topology
No comments:
Post a Comment